La regressione è un processo statistico che ci permette di stimare le relazioni tra variabili. Determina il legame funzionale tra le variabili indipendenti e le variabili dipendenti.
La regressione corrisponde al valore medio atteso in base ai dati di input che noi immettiamo. Grazie alla regressione si può parlare di previsione sui valori attesi.
I valori di ingresso sono un vettore di dati n-dimensionale dalla quale deriva un unico valore di uscita, determinando così l'operazione di regressione.
I modelli di regressione
Gli algoritmi supervisionati fanno uso di un insieme di campioni e per ogni campione abbiamo l'output corretto.
L'output corretto è associato ad ogni campione di input.
Davanti a questo tipo di situazioni abbiamo un problema supervisionato.
Tra i problemi supervisionati abbiamo due categorie principali: una è la regressione, l'altra è la classificazione.
La regressione consiste nello stimare un valore reale (continuo), mentre la classificazione genera un valore discreto.
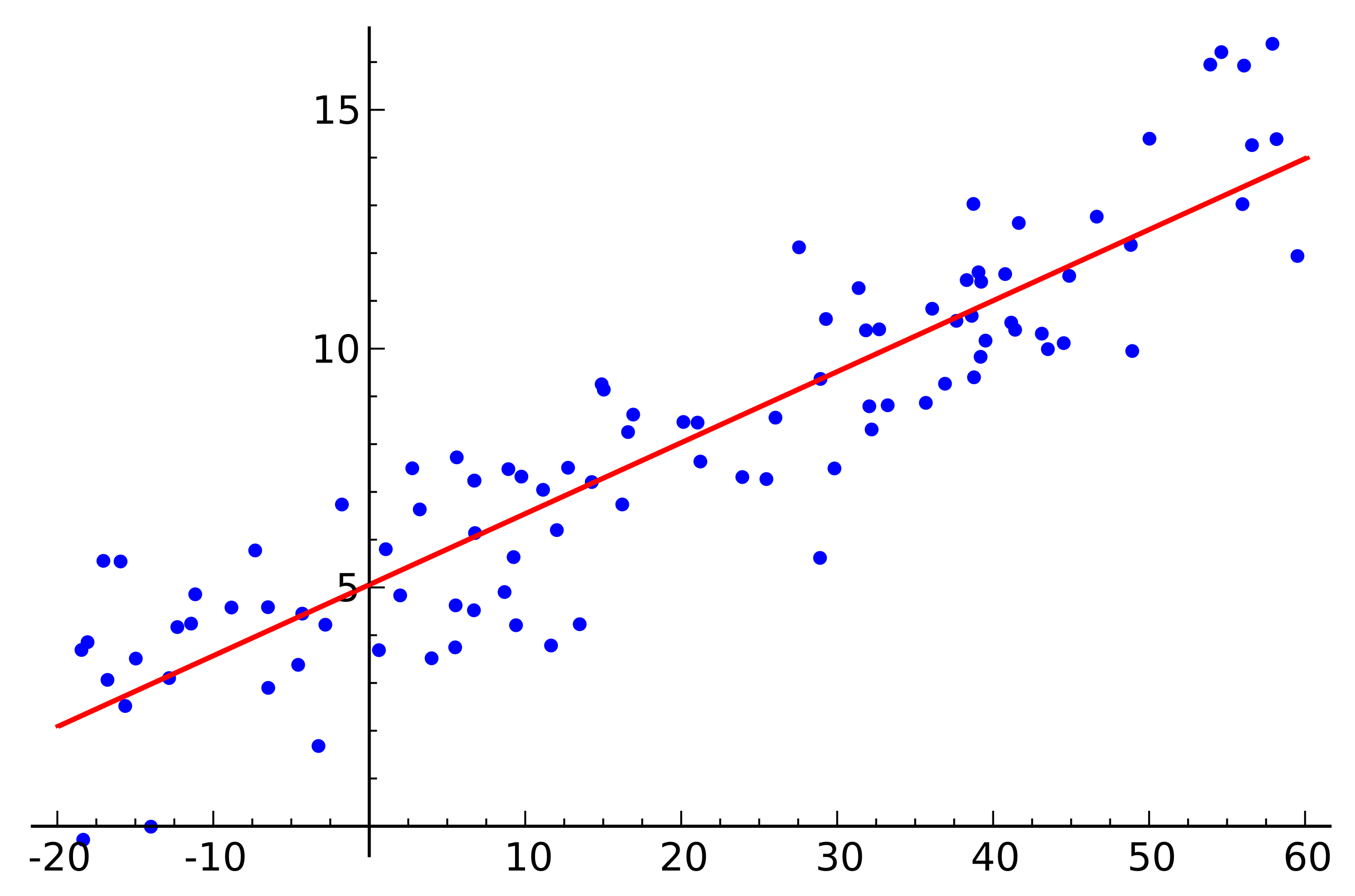
1) Regressione lineare - quando la relazione tra le variabili indipendenti è di tipo lineare, abbiamo una regressione lineare.
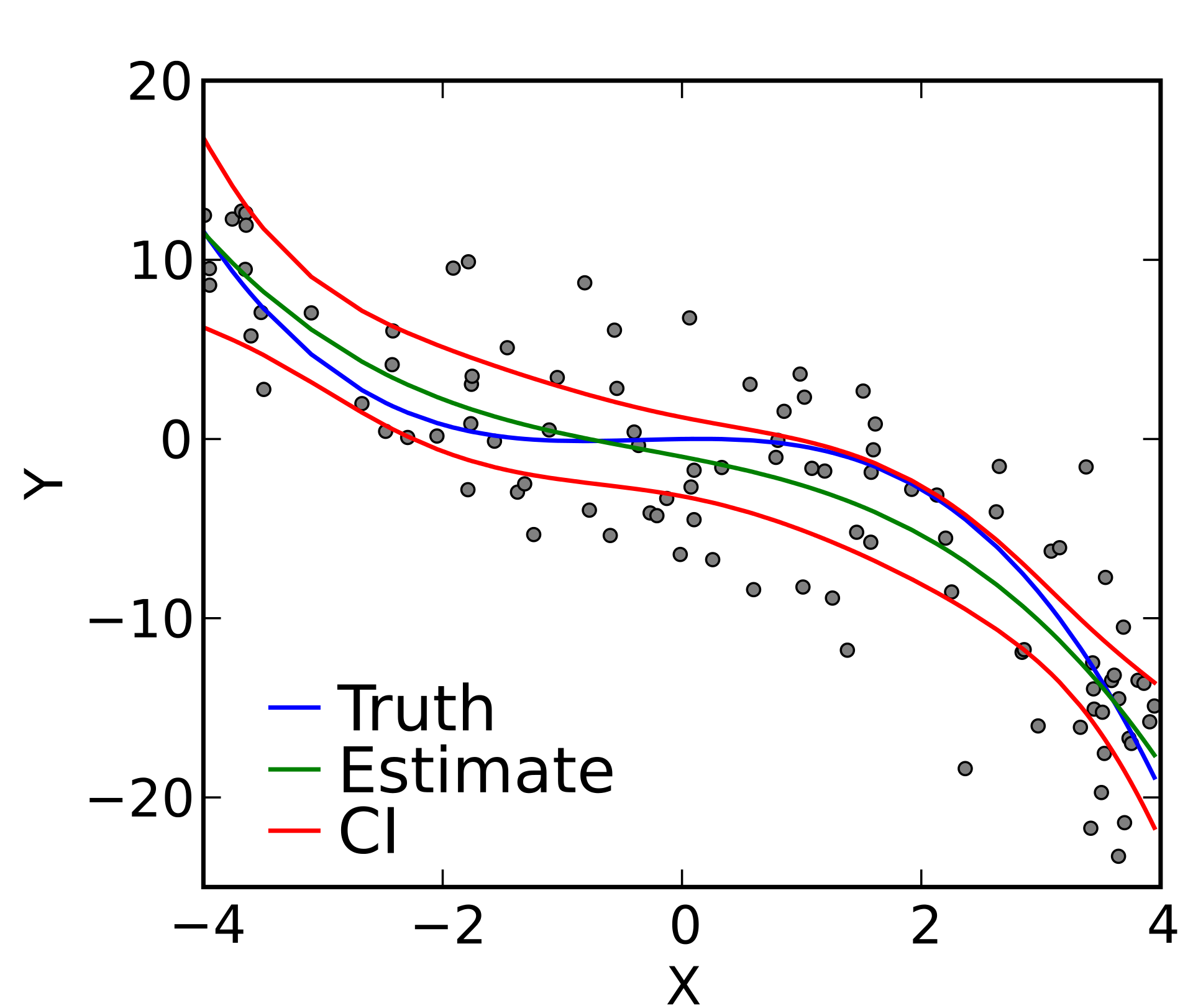
2) Regressione polinomiale - la funzione che collega le variabili indipendenti dalle variabili dipendenti è un polinomio.
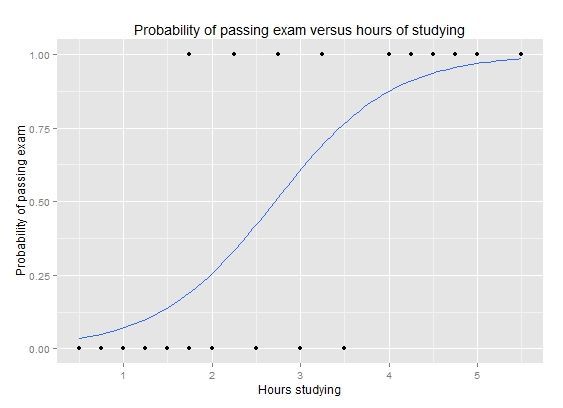
3) Regressione logistica - dalla regressione si vuole ottenere l'individuazione di una proprietà appartenente alle variabili indipendenti. Rileva se tra i dati di input c'è la presenza di una determinata proprietà.
4) Regressione non parametrica / Semi parametrica - hanno come oggetto di interesse una caratteristica della distribuzione condizionata della variabile dipendente
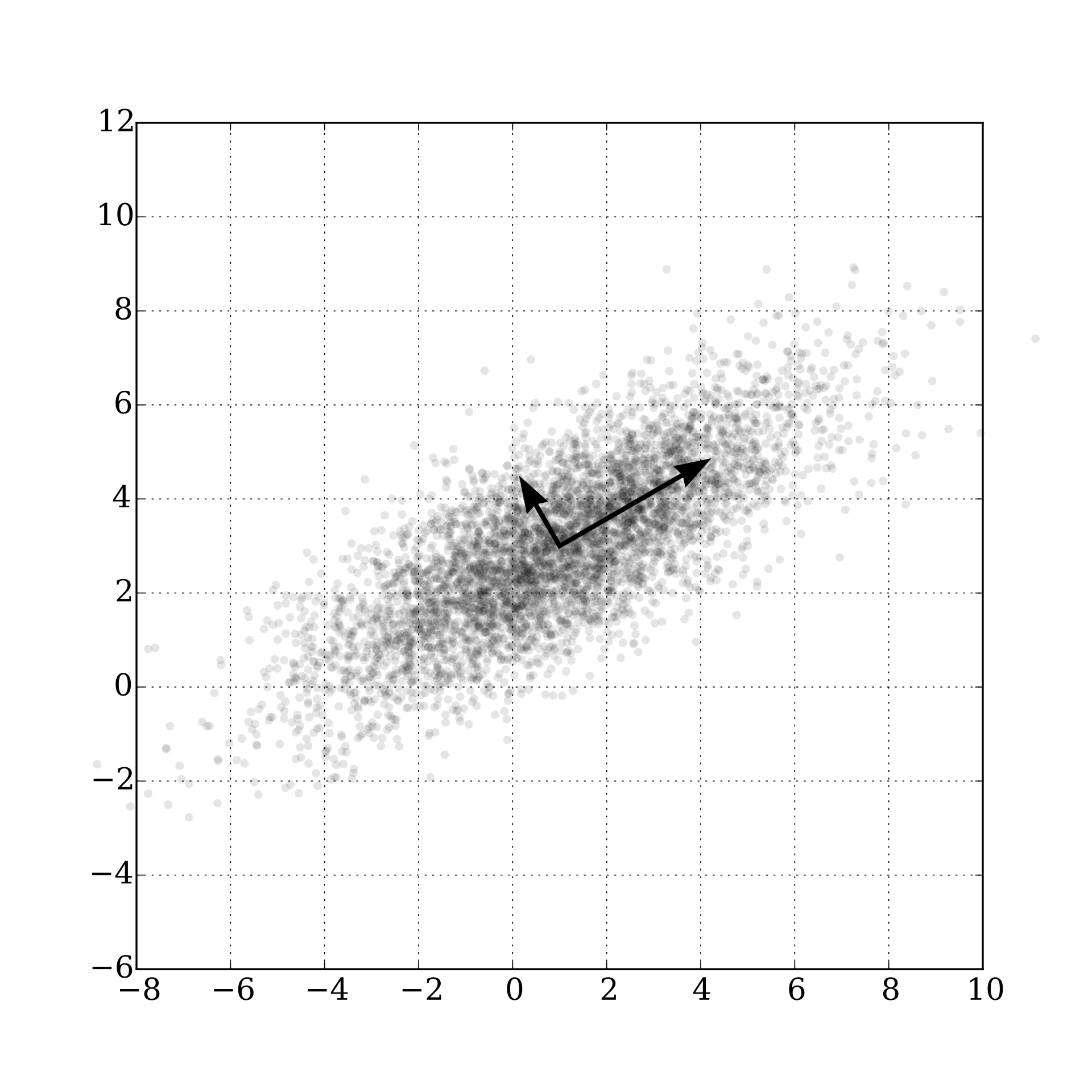
5) PCA (Principal component analysis) / Encoding - è una procedura che utilizza la trasformazione ortogonale per convertire un set di variabili correlate in un set di variabili lineari non correlate chiamate "principal components".